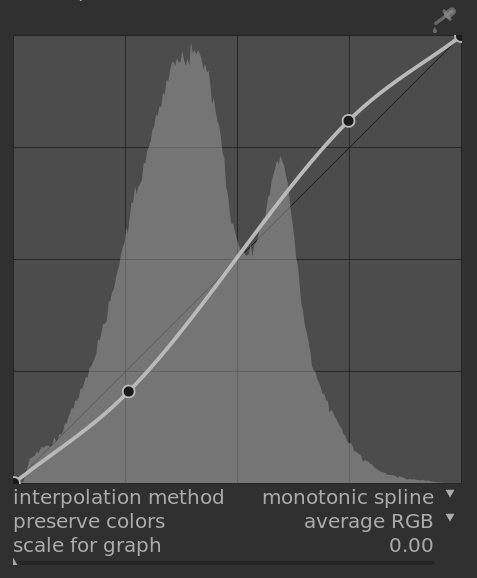
Kurven
Die Module Basiskurve, Farbkurve und RGB-Kurve nutzen Kurven, um die Farbtöne im Bild zu steuern. Diese Module haben einige Gemeinsamkeiten, die eine separate Besprechung rechtfertigen.
🔗Knoten
In ihrem Standard-Status sind Kurve gerade Linien, die zwei Anker-Knoten oben rechts und unten links der Grafik definiert sind. Du kannst die Knoten bewegen, um die Kurve zu verändern, oder mit klicken auf die Kurve zusätzliche Knoten generieren. Mit Strg+Klick um einen neuen Knoten an der x-Lokation des Mauszeigers und der zugehörigen y-Lokation – das wird einen Knoten hinzufügen ohne das Risiko einer ungewollten Änderungen der Kurve. Es können bis zu 20 Knoten pro Kurve definiert werden. Um einen Knoten zu entfernen, klicke darauf und ziehe in aus dem Kurvenbereich.
🔗Kurven Eigenschaften
Die folgenden Bedienelemente haben zwei oder mehr der obigen Dunkelkammer-Module gemeinsam und sie werden hier deshalb separat vorgestellt. Die Dokumentation der einzelnen Module beinhaltet ggf. weitere Bedienelemente.
- Interpolations-Methode
- nur für Tonwert Kurve und RGB Kurve
-
Interpolationen sind ein Prozess, bei welchem eine fortlaufende Kurve durch eine Reihe von Knoten definiert wird. Da dieser Prozess nie ganz perfekt ist, gibt es mehrere Methoden, die das abmildern können, für Probleme, die du finden könntest.
-
- kubische Spline ist davon sicher die visuell am meisten gefällige. Weil sie weiche Kurven gibt, wird der Kontrast im Bild besser aufgebessert. Diese Methode ist aber sehr sensitiv zur Postion der Knoten und kann Scheitelpunkte und Oszillationen verursachen an Orten, wo die Knoten sehr nahe beieinander sind, oder wenn es zu viele davon gibt. Die Methode ergibt die besten Resultate mit 4 bis 5 Knoten, die gleichmäßig verteilt sind.
-
- Die _zetripetale Spline ist spezifisch dafür berechnet Scheitelpunkte und Oszillationen zu verhindern, wird aber als Nachteil den Knoten weniger genau folgen. Sie ist sehr robust ungeachtet von der Anzahl der Knoten, sie wird aber einen faderen und dumpfen Kontrast ergeben.
-
- Die gleichbleibende Spline ist spezifisch dafür geschaffen eine gleichbleibende Interpolation zu geben, was bedeutet, dass es keine Oszillationen gibt, wo die kubische Spline solche produzieren kann. diese Methodei ist die am besten geeignete, wenn du versuchst eine analytische Funktion einer Knoten-Interpolation zu schaffen (zum Beispiel: exponentielle, logarithmische, usw.) solche Kurven werden als Voreinstellungen vorgesehen. Es ist ein guter Mittelweg zu den früher ausgesprochenen Methoden.
- Erhalte Farben
- Falls eine nicht lineare Tonkurve bei jedem RGB Kanal einzeln angewendet wird, kann es sein, dass der Anteil der Angleichung für jeden Kanal unterschiedlich ist und so der Farbton sich verschiebt. In der Schaltbox Erhalte Farben gibt es unterschiedliche Methoden das “Luminanz-Niveau” der Pixel zu berechnen, um diese Versatze zu minimieren. Der Anteil der Angleichung des Farbtones wird aus seinem Luminanz-Wert errechnet, und dann wird die gleiche Angleichung an alle drei RGB Kanäle angewendet. Unterschiedliche Helligkeitsdetektoren können den Kontrast in verschiedenen Teilen des Bildes beeinflussen, abhängig von den Charakteristiken des Bildes. Der Nutzer kann deshalb den Detektoren wählen, der das beste Ergebnis für ein bestimmtes Bild liefert. Einige dieser Methoden werden im Detail behandelt in den Einstellmöglichkeiten von erhalte die Chrominanz im Modul Filmic RGB. Es gibt da die folgenden Optionen:
-
- keine
- Luminanz
- max RGB
- durchschnittlich RGB
- Summe RGB
- Norm RGB
- grundlegende Stärke
- Skala für die Grafik
- Nur für Tonwert Kurve und Basiskurve
-
Die Skala erlauben es dir die Grafik-Anzeige zu verzerren, sodass gewisse grafische Eigenschaften dir helfen nützlichere Kurven zu zeichnen. Beachte, dass die Option Skala nur die Anzeige der Kurve betrifft und nicht die aktuellen Parameter, die im Modul gespeichert sind.
-
Standardmäßig wird ein “linearer” Maßstab genutzt (definiert durch einen Skalierungsfaktor von 0) mit gleichverteilten Abszissen- und Ordinatenachsen.
-
Eine logarithmische Skala wird die hohen werte komprimieren und die tiefen Werte auseinanderziehen, sowohl der Abszissen und der x-Achsen, sodass die Knoten der dunklen teile auf der Grafik mehr Platz bekommen und so besser kontrolliert werden können.
-
Der Regler ‘Skalierungsfaktor’ verändert die Basis des Logarithmus, mit dem die Achsen skaliert werden. Damit steuert er die Wirkung der Skalierung bezüglich einer Stauchung bzw. Streckung. Werden nur exponentielle oder logarithmische Funktionen von Identitätslinien gezeichnet, definiert der Reglerwert die Basis der Funktionen.